This writing is posted as a service to the Canadian
public and interested persons elsewhere
additinal information may be available from Cellular
Alert Canada
determining the endangered area at transmitter towers for a worst case of mechanical failure.
The transmitter towers for telecommuniction are normally from 200 ft
(ca. 60m) to 350 ft (ca. 100m) high, and in some cases even more, depending
on the local elevation. To accomodate the construction a site is
required, being a square with a sidelength of about twice the towers height.
However, if available properties in desired locations are not big enough
to accommodate this, in an area with lower wind activity the steel ropes
( guys), that hold the tower in place, are set at a steeper angle requiring
a smaller area for construction, thus the square size is reduced allowing
the use of a smaller piece of property. In higher wind load areas, where
a steeper angle may not secure the tower safely, a big enough site must
be found. But according to the local office of Industry Canada in Belleville,
ON the above outlined square size is not regulated and since those towers
are considered utility structures local building codes do not apply..
The size of the square depends only on the area needed for the actual construction of the tower with the anchors. Furthermore, the size of the security area (fence) is set to protect the site from outside hazards, and not to protect the public from hazards caused by the installation. This distance by itself is therefore inadequate as a safety zone, because it is does not give a safe area in case of a serious mechanical failure at the tower. This is a serious flaw in the site selection process.
The following calculations are based on a worst case scenario to determine the area endagered in such a situation by mechanical failure at the tower. We assume for a worst case scenario a total mechanical failure that can be caused by stress, extreme overload, defect in material, fatige, corrosion, poor workmanship, insufficient maintenance, and sabotage, as well as any combination of these factors.
In the following calculations the letter h represents the height of a given tower.
For a rigid structure (e.g. a pole or even a tree) the endangered zone is a circle with a radius of the structure’s ( tower ) height, that is twice the height in diameter, it is accomodated by a square with such a sidelength, that is 2 x h. Most sites have exactly this size and are therefore declared sufficient by the operating company.
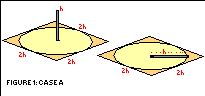
However, most of these towers are not single pole structures; they are cage element structures secured with steel ropes (guy wires) to ground anchors. The possible hazards of these wires add to the endangered area. The upper ones of these wires are reaching up to at least about 90% of the height of the tower, that is 0.9 h. They are secured to an anchor in the ground that is positioned within the square. For the calculations the anchors are assumed to be at a distance equal to 90% of the height from the center of the tower, that is also 0.9 h. The length of the highest reaching wires calculates then to about 1.27 times the height of the tower, that is 1.27 h.
(apply Highschool Math -[ Pythagoras]: guy wire length = sqare-root of { (0.9 h) ² + (0.9 h) ²} = 1.27 h )
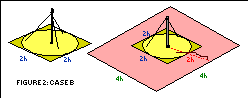
The whip-lashing and falling steel rope endangers an area with a radius
given by it’s length around the anchor. The guy anchors are assumed to
be located at 90% of the height, that is 0.9 h , from the center of the
tower. Therefore the endangered zone is 0.9 h + 1.27
h = 2.17 h reaching 1.17 h outside
the normal tower site (a 2 h square).
With tie wires this risk could be reduced, but a tie wire may give way
under such conditions too. The theoretical distance endagered by such a
wire is therefore 2.17 h from the tower center. Taking in
account bends in the falling wire and obstructions in the path, a reasonable
reduction of this distance by 10 % can be made. The real danger zone for
mechanical failure is therefore 90% of this distance, that is 0.9 x 2.17
h = 1.953 h , rounded to 2.0 h, from the center of
the tower. The danger area is a circle with 4 h in diameter
Therefore, only if the site is a square with a side of at least 4 times
the height of the tower, it encloses the danger zone in case of severe
mechanical failure!
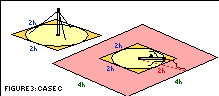
CASE C) The wires snap at the anchor, and the tower falls.
The falling tower causes the guy wires to whip out in the direction
of its fall. The longest wire is connected at 90% of the towers height.
Hence, the calculations have the same numbers and the result as in case
B). The distance of danger is 2 x h from the center of the
tower. The radius of danger is given by this distance = 2 h.
The area is a circle with 4 h in diameter
Again here, only a square with a side of 4 times the height of the tower
encloses the danger zone.
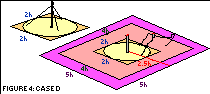
CASE D) The top wire snaps at one anchor the top cage element breaks off and lashes out tied to a remaining anchor .
The total mechanical length is 2x wire length plus anchor distance from
center that calculates to (0.9 + 2.54) h = 3.44 h
applying bend and drag reduction the safe distance in this case easily
calculates to 0.9 h + 0.9 x 1.27 h + 0.4 x
1.27 h = (0.9+1.143 + 0.508) h =2.551 h.
The safety zone is a circel with about 5 h in diamenter
requiring a squre of this side length .
The 40% drag-lash length is a favourable assumption - applying the full
length of this "debris" 3.44 h from center would require
a square of about 7 h to ensure 100% safety.
The fenced area may be smaller, depending on regulations, but the tower
must then be removed from a neighbouring property by the above calculated
lengths to be at a safe distance.Therefore, any such tower should be distanced
at least twice the height better two and a half times the towers
height from any neighbouring property line or even road!
However, no such regulation is currently given.
If in your neighbourhood a tower is built
make sure the above calculations are respected - nothing less
this is your legal right
and the tower people know it !
Simply ask for proof of a signed and verified insurance
even in case of sabotage at the tower. . .
you can let a judge decide how much liability they have to cover
copyright © 1997 by Wolfgang W. Scherer
for comments or questions e-mail the author Wolfgang W. Scherer